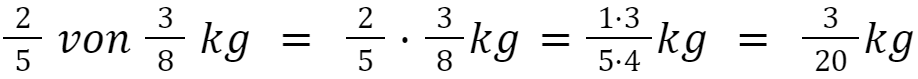Grundbegriffe
Brüche haben die Form z/n mit z ∈ IN und n ∈ IN.
z heißt der Zähler, n heißt der Nenner des Bruches.
Zu jedem Quotienten z : n gibt es eine Bruchzahl z/n
Beispiel:
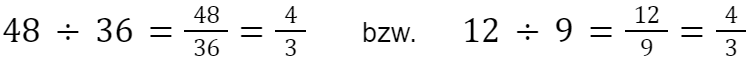
Einführung:
Brüche sind aus unserem Alltag nicht mehr wegzudenken: ein Viertel, ein Drittel, ein Achtel, ein Halb(es), drei Viertel. All dies sind Brüche die tagaus tagein benutzt werden. Um mit Brüchen später leichter rechnen zu können, werden diese in der oben dargestellten Art und Weise aufgeschrieben.
Ein Bruch macht nur Sinn, wenn er auf etwas bezogen wird. Sonst würde nur jemand sagen: "Ein Drittel!". Diese Aussage ist sinnlos, da nicht mitgeteilt wurde von was ein Drittel genommen werden soll. Sinnvolle Aussagen sind dagegen:
"Ein Drittel von einem Liter Limo",
"eine Viertel Stunde",
"ein halber Kilometer".
All diese Größen wurden also zunächst in gleichgroße Stücke unterteilt und eines dieser Stücke wurde genommen. Als Bruch geschrieben ergäbe sich:
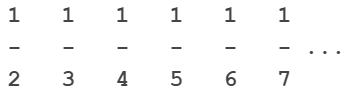
Somit kommt bei einem Bruch dem Nenner die größte Bedeutung zu. Er gibt an, in wie viele gleichgroße Teile ein Ganzes geteilt wird.
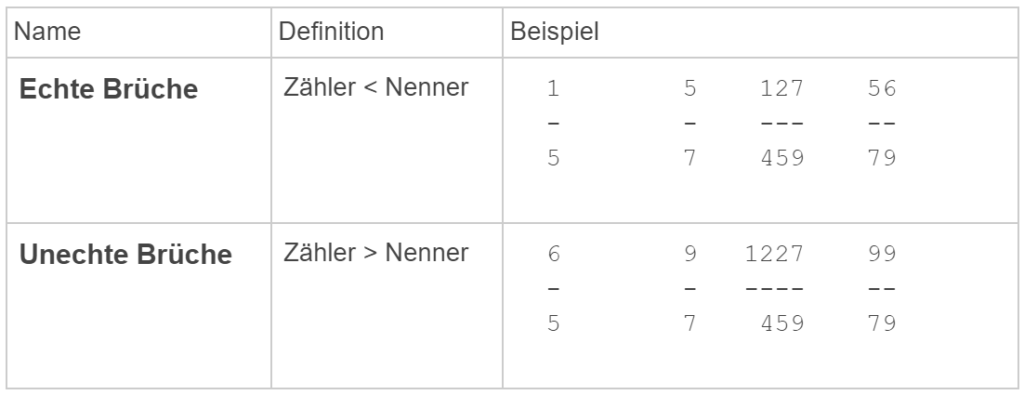
echte und unechte Brüche
Scheinbrüche

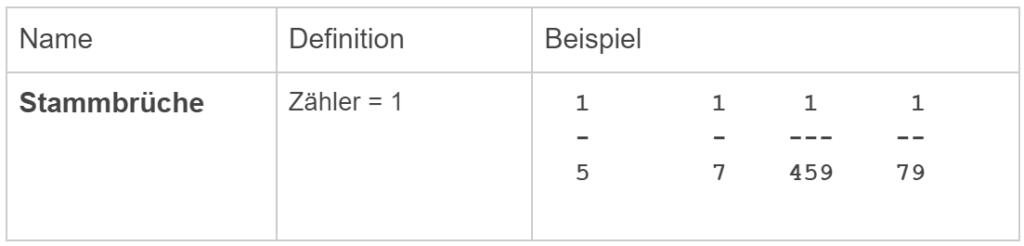
Stammbrüche
Gemischte Zahlen
Ist bei einem Bruch der Zähler größer als der Nenner, so kann man ihn als gemischten Bruch bzw. gemischte Zahl schreiben:
Beispiel:
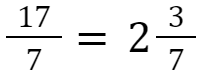
Gleichwertige Brüche
Manchmal kann es sein, dass Brüche mit unterschiedlichen Nennern dennoch den gleichen Wert am Zahlenstrahl markieren. Solche Brüche nennt man gleichwertige Brüche. Sie beschreiben die gleiche Menge Kuchen. So sind im obigen Beispiel folgende Brüche gleichwertig:
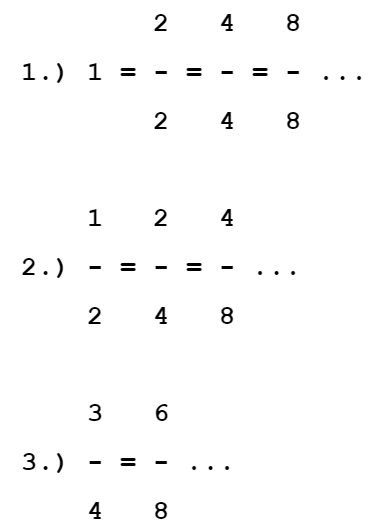
Selbst mit der Zahl 0 funktioniert dies:
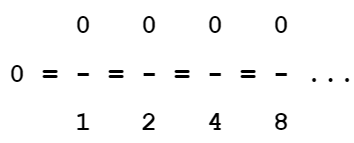
Die drei Punkte ... sollen andeuten, dass es unendlich viele gleichwertige Brüche zu jeder Stelle am Zahlenstrahl gibt, da sich jedes Kuchenstück z.B. wieder teilen lässt.
Erweitern und Kürzen
Zu jeder Bruchzahl gehören unendlich viele verschiedene Brüche.
Beispiel:
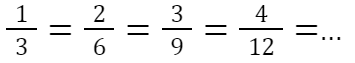
Erweitern heißt Zähler und Nenner mit der gleichen Zahl multiplizieren.
Der Wert der Bruchzahl ändert sich dabei nicht
Beispiel:
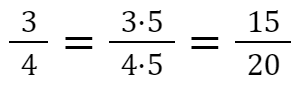
Kürzen heißt Zähler und Nenner durch die gleiche Zahl dividieren.
Der Wert der Bruchzahl ändert sich dabei nicht.
Beispiel:
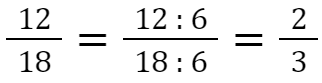
Ein Bruch, den man nicht mehr kürzen kann, nennt man vollständig gekürzt.
(Grundform des Bruches)
Brüche addieren und subtrahieren
Gleichnamige Brüche (=gleicher Nenner) werden addiert bzw. subtrahiert,
indem man die Zähler addiert bzw. subtrahiert und den Nenner beibehält.
Beispiel:
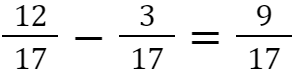
Ungleichnamige Brüche (=verschiedene Nenner) müssen vor dem Addieren bzw. Subtrahieren zuerst gleichnamig (=nennergleich) gemacht werden.
Beispiel:
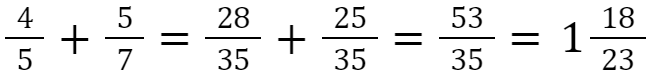
Brüche multiplizieren
Zwei Brüche werden miteinander multipliziert, indem man je die Zähler und die Nenner miteinander multipliziert.
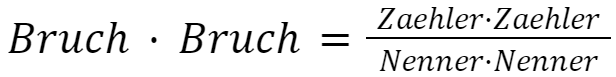
Beispiel:
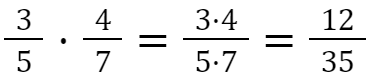
Gemischte Zahlen müssen vor dem Multiplizieren in unechte Brüche verwandelt werden
Merkregel:
Wird eine Zahl mit einer ganzen Zahl (z.b. 3, 17, 20) multipliziert, so wird die ursprüngliche Zahl größer.
Wird eine Zahl mit einer echten Bruch (z.b. 1/3, 3/5, 17/38) multipliziert, so wird die ursprüngliche Zahl kleiner.
Brüche dividieren
Zwei Brüche werden durcheinander dividiert, indem man den ersten Bruch mit dem Kehrwert des zweiten Bruches multipliziert.
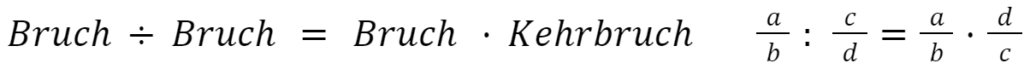
Beispiel:
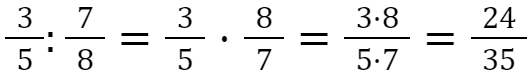
Brüche vergleichen
Von zwei Brüchen mit gleichem Zähler ist derjenige der größere, der den kleineren Nenner hat.
Beispiel:
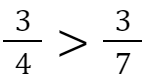
Von zwei Brüchen mit gleichem Nenner ist derjenige der größere, der den größeren Zähler hat.
Beispiel:
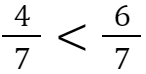
Brüche mit verschiedenen Nennern bringt man vor dem Vergleichen normalerweise auf den
Hauptnenner ( = kgV aller Nenner). Diesen Schritt nennt man auch „gleichnamig machen“.
Gemischte Zahlen addieren und subtrahieren
Sowohl bei der Addition als auch bei der Subtraktion bietet es sich jedoch an die gemischten Brüche bei zu behalten.
Sind zwei Brüche als gemischte Brüche gegeben, so addiert subtrahiert man diese nach folgendem Schema:
1. Die Teilbrüche werden auf den Hauptnenner gebracht.
2. Die ganzen Zahlen werden addiert und die Zähler werden addiert.
2. Ist der Zähler des ersten Bruchs größer als der Zähler des zweiten, so wird beim ersten Bruch ein Ganzes abgezogen und zum Teilbruch addiert.
3. Aus dem Teilbruch werden eventuell Ganze herausgezogen.
4. Der Teilbruch wird gekürzt.
Natürlich kann man auch die gemischten Brüche erst in unechte Brüche umwandeln und dann normal addieren.
Beispiel
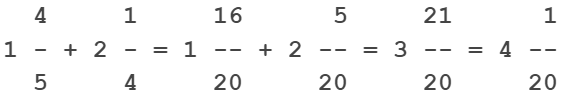
Beispiel
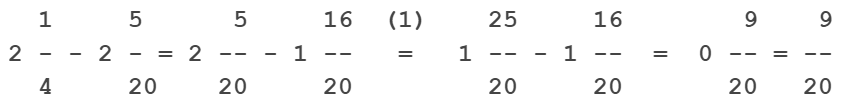
An der Stelle (1) wurde von den 2 Ganzen des ersten Bruchs 1 Ganzes weggenommen, in 20/20 umgewandelt und zum Teilbruch addiert. So können die Zähler problemlos subtrahiert werden.
Bruchteile von Größen
Bei Anteilen bedeutet “von“ so viel wie „ “.
Beispiel: