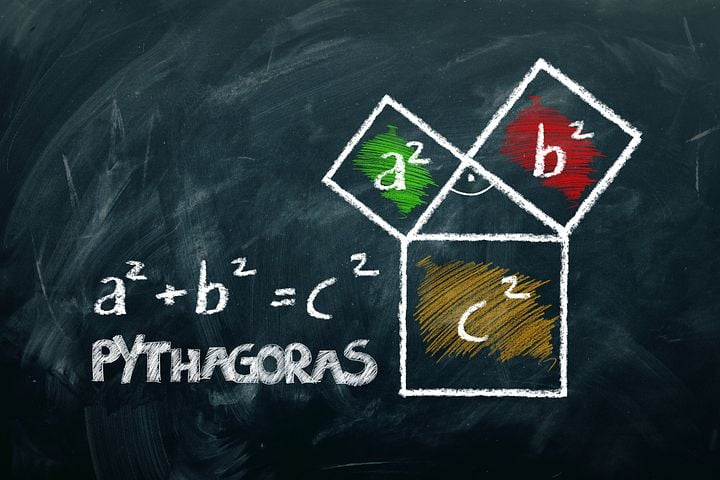
Ein Dreieck, bei dem ein Winkel 90° beträgt, nennen wir rechtwinkliges Dreieck. In rechtwinkligen Dreiecken gibt es eine lange Seite (die sogenannte Hypotenuse) und zwei kürzere Seiten (die sogenannten Katheten). Der Satz des Pythagoras ist eine besondere Regel für solche rechtwinkligen Dreiecke.
Mit dem Satz des Pythagoras kannst du die Länge einer Seite in einem rechtwinkligen Dreieck finden, wenn du die Längen der anderen beiden Seiten weißt.
Wenn du die Länge der beiden kürzeren Seiten quadrierst (also jede Länge mal sich selbst multiplizierst) und die beiden Ergebnisse zusammenzählst, erhältst du genau das gleiche Ergebnis, als wenn du die Länge der längsten Seite quadrierst.
Mathematisch ausgedrückt: a² + b² = c²
Der Satz des Pythagoras ist nach dem antiken griechischen Mathematiker Pythagoras benannt, der das Theorem vermutlich nicht selbst entdeckt hat, aber dessen Schule es bekannt gemacht hat.
Eine gute Möglichkeit, sich den Satz des Pythagoras zu merken, ist es, sich ein rechtwinkliges Dreieck mit den Seitenlängen 3, 4 und 5 vorzustellen. Dieses Dreieck ist ein Beispiel für ein sogenanntes "pythagoreisches Tripel". Da 3² + 4² = 9 + 16 = 25 und 5² = 25 ist, erfüllt dieses Dreieck die Bedingungen des Satzes des Pythagoras.
Der Satz des Pythagoras hat zahlreiche praktische Anwendungen in verschiedenen Bereichen wie Bauwesen, Architektur, Landvermessung, Navigation und Physik. In all diesen Bereichen ist es oft notwendig, Längen und Abstände zu berechnen, die auf rechtwinkligen Dreiecken basieren.
Die Kenntnis des Satzes des Pythagoras verbessert das räumliche Vorstellungsvermögen und das Verständnis von Raumgeometrie. Die Formel a² + b² = c² solltest du auswendig lernen und im Halbschlaf aufsagen können. Diese Formel musst du auch für deine Abitursprüfung wissen.
Um dich auf eine Klassenarbeit zum Satz des Pythagoras vorzubereiten, empfehlen wir dir auch, mit echten Klassenarbeiten anderer Schüler zu üben. Entsprechendes Übungsmaterial findest du kostenfrei auf der Webseite www.klassenarbeiten.de