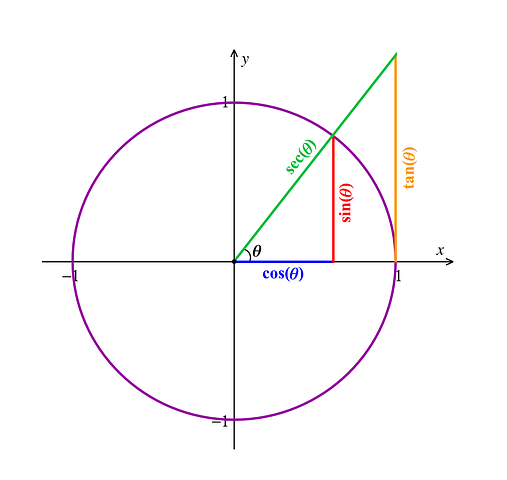
Die Trigonometrie ist ein Teilgebiet der Mathematik, bei der es um die Beziehungen zwischen den Seiten und den Winkeln von Dreiecken geht. Mithilfe der Trigonometriefunktionen kannst du beispielweise unbekannte Seitenlängen oder Winkel in rechtwinkligen Dreiecken berechnen, wenn andere Größen gegeben sind.
Je nachdem welche Größen gegeben sind, musst du die richtige Formel auswählen und verwenden:
Sinus(α) = Gegenkathete (gegenüberliegende Seite) / Hypotenuse (längste Seite)
Kosinus(α) = Ankathete (anliegende Seite) / Hypotenuse (längste Seite)
Tangens(α) = Gegenkathete (gegenüberliegende Seite) / Ankathete (anliegende Seite)
Jedes rechtwinklige Dreieck hat eine längste Seite. Diese wird Hypotenuse genannt. Die zwei kürzeren Seiten, werden als Katheten bezeichnet. Wenn du beispielsweise einen der Winkel in diesem Dreieck sowie die Länge der Hypotenuse kennst (außer dem 90-Grad-Winkel), kannst du die Längen der anderen Seiten mithilfe von Sinus, Kosinus und Tangens herausfinden.
Mit der Trigonometrie kannst du auch im realen Leben Probleme lösen. So lässt sich beispielweise die Höhe eines Baumes berechnen, ohne dass du auf ihn hinaufklettern musst. Was benötigst du dazu und wie funktioniert das?
Zunächst benötigst du einen Maßstab, ein Maßband und ein Werkzeug zum Messen von Winkeln (z.B. einen Neigungsmesser oder eine Smartphone-App).
Suche dir nun einen Punkt auf dem Boden aus, von dem aus du den Baum gut sehen kannst. Achte darauf, dass der Boden zwischen dir und dem Baum relativ eben ist.
Stehe an dem ausgewählten Punkt und richte den Maßstab oder das Winkelmessgerät auf die Baumspitze. Miss den Winkel zwischen dem Boden und der Sichtlinie zur Baumspitze. Dieser Winkel wird α (Alpha) genannt.
Miss die Entfernung zwischen dir und dem Baum mit dem Maßband. Nennen wir diese Entfernung "A".
Miss auch deine Augenhöhe vom Boden aus. Nennen wir diese Höhe "H".
Jetzt hast du alle Informationen, die du benötigst, um die Höhe des Baumes mithilfe der Trigonometrie zu berechnen. Du wendest die Tangens-Funktion an, die das Verhältnis der Gegenkathete zur Ankathete angibt:
tan(α) = Höhe des Baumes (ohne deine Augenhöhe) / Entfernung zum Baum
Löse die Gleichung nach der Höhe des Baumes auf:
Höhe des Baumes (ohne deine Augenhöhe) = A * tan(α)
Zum Schluss addiere deine Augenhöhe "H" zur berechneten Höhe, um die Gesamthöhe des Baumes zu erhalten:
Gesamthöhe des Baumes = (A * tan(α)) + H
Nachdem du die Berechnung durchgeführt hast, erhältst du die geschätzte Höhe des Baumes. Die Methode ist zwar nicht perfekt, aber sie gibt dir eine ziemlich gute Schätzung der Höhe des Baumes. Und das ohne dass du auf den Baum hinaufklettern oder den Baum fällen musst.
Trigonometrie ist generell ein sehr nützliches Werkzeug zum Lösen von Problemen im Zusammenhang mit Winkeln, Entfernungen und Höhen. Sie findet daher auch beispielweise in den Bereichen Architektur, Ingenieurswesen, Geologie und Kartographie, Astronomie, Physik und Computergrafiken viele Anwendungsfälle.